A Quick lesson on MOD

In our everyday life we see things that repeat once we get to a certain point. For example, let us say you have 463 eggs. How many dozens of eggs can you make? How many would be left over? We know this a division. We know that if we take 463 and divide by 12 will we receive 38 with a remainder of 7. Thus we have 38 dozens plus 7 eggs left over. Same thing with warehouses. Let us say you must pack 40 widgets into a box and the rest will go into a shipment bag. You are to prepare 7343 widgets for shipment. How many boxes will you need? How many widgets will be in the bag? Excel provides a function that is rarely used, but if perfect for instances where we need to indicate a cycle like feature into calculations. That function is called MOD. Let's look at the parameters for MOD: =MOD(number, divisor) Both parameters are required. The number is the number you wish to divide, and the divisor is the number that you are dividing by. In essence, this function will return the remainder of the divide. So if we were to say =MOD(463,12) we would receive the number 7 as our answer. I know what you are thinking, "Oh wow, that seems pretty useless." Let's graph mod shall we?

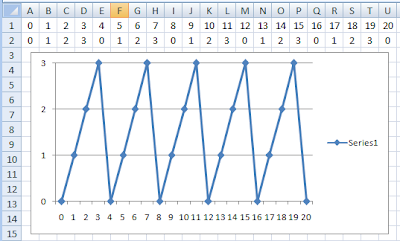
Here we are using a MOD 4. So the numbers repeat 0, 1, 2, 3, 0, 1, 2, 3 ... You can see the cyclical nature of MOD from the graph. So anything that requires a calculation with a cyclical nature can usually be solved pretty easily with MOD. The trouble is trying to wrap your head around the notion of, "What is cyclical?" Sometimes it is not very obvious that we are talking about something that keeps repeating. Let's take an example of something I learned in Algebra II in high school. Let us say you are tasked to be given a number, you must find the next highest number that is a multiple of fourteen. You are then to take that next highest number and figure out the difference between that number and the number given. You might see this in the real world as, "I want all my widgets to come in boxes, boxes hold 14 per box. I may order something that is not a multiple of 14. Therefore, you are increase the order to the next highest multiple of fourteen." Here the cycle is 14. We need to make a box every time we hit fourteen. If the order comes in at 15, we know that we need to up the order by 13 to 28, since 14*2 = 28. However, how do we make Excel do this kind of calculation? We know that =MOD(15,14) will give us 1. We could then say 14-1 = 13 + the order = 28. Thus if our ordered number is cell A1 and our fill amount is A2, then the next highest number could be in cell A3: =A2-MOD(A1,A2)+A2 However, there is a problem with that. It stops working correctly if the number ordered is indeed a multiple of 14. So if we say the customer has ordered 28, then we need not calculate anything because 28 is a multiple of 14. So how do we work around this? We could use an if statement, but that doesn't seem very elegant. This is where my high school algebra class comes into play. Remember that mod is a cycle. What we truly need is how far away are we from reaching a multiple of 14. So if the order is 1, we are 13 from a full box; if the order is 7, we are 7 from a full box; if the order is 14, we are zero from a full box. So we know that =MOD(13,14) would give us 13, which is pretty much what we want the answer to 1 to be. So let's try =MOD(1*13,14). Since the number eventually comes out to be 13, we basically say that 1 is 13 steps from 14. Let's try 2 which is 12 steps from 14. =MOD(2*13,14), which happens to be 12! You will see that =MOD(A1*(A2-1),A2) will always tell you the number of steps you are from reaching the next highest number. Let's graph it:

As you can see, the cycle repeats in the red line. Now I'm cheating here, because I didn't give you the math as to why this is. However, now that you are armed with that knowledge, I'll leave proof to the reader. You can now say that =MOD(A1*(A2-1),A2)+A1 There you go! Now you have a formula that will work for your customer.